分析电阻应变式传感器蠕变特性，利用其加/卸载和蠕变输出变化率的不同，判断蠕变起始点，根据蠕变过程和零点变化的特点进行蠕变跟踪，以此确定传感器实际载荷。此方法简单方便，易于实现。

　　传感器精度高低是决定天平精度高低的主要因素。目前高精密电子天平大部分采用磁悬浮式的传感器设计，而低成本的应变式传感器只能用于低精度的电子天平。影响电阻应变式传感器精度的主要原因之一是这种传感器的蠕变指标。传感器蠕变是由弹性体产生的正蠕变、应变片和应变胶负蠕变综合影响而形成的。一般来讲，弹性体设计定型后，其蠕变值也大致确定，控制和调整蠕变的传统做法是选用不同蠕变补偿性能的应变片，改变贴片位置和粘胶固化工艺等方法来实现。这种靠调节制造工艺等方法来调控蠕变，其工艺过程繁复，返工量大且随机性高。笔者多年来对传统应变式传感器内部性能进行深入细致的研究，结合目前先进的数据采集技术（利用∑-ΔA/D转换器），应用单片机技术实现了对传统应变式传感器输出信号进行高性能数字滤波、动态蠕变跟踪，零点漂移跟踪。使原本只能用于低精度场合的应变式传感器的测量精度大大提高（可优于1/30000）。应用该技术设计的精密电子天平较磁悬浮式电子天平有更高的性价比。

　　保持温度恒定，在某一恒定机械应变长期作用下，传感器输出随时间变化的特性，称为传感器蠕变。在不承受载荷的条件下，传感器随时间变化的特性称为零漂。零漂是不承受载荷条件下的蠕变。称重传感器的蠕变特性曲线如图1所示（以正蠕变为例，负蠕变与正蠕变相类似），其中曲线L为传感器的加载特性曲线，曲线C为传感器的卸载特性曲线。从中可以看出，传感器的加载曲线由加载段L0和蠕变段L1组成。在加载段L0，传感器的输出急剧增加，迅速达到载荷的真实变化值W0，

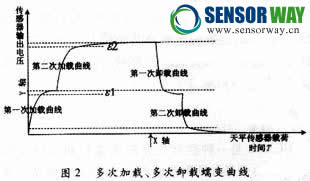
　　图中用S1点表示，在这个时间段，由于时间极短，传感器产生的蠕变较小；进入L1段后，传感器输出发生缓慢的增加并逐渐趋近不变，蠕变值ε随时间动态变化；在传感器卸载曲线C上，卸载曲线由卸载段C0和蠕变恢复段C1组成，传感器输出值以极高的速度迅速衰减到卸载曲线的S2点，超过S2点，传感器输出缓慢回零，蠕变恢复值ε也是随时间动态变化的，并逐渐趋近零点不变。电子天平的称重值是加载在传感器上的载荷值减去传感器在天平零点时的载荷值。从以上分析来看，我们假定蠕变和蠕变恢复是相等的（实际中有相当多传感器这两个阶段可认为近似相等），也就是说，图1所示的L1和C1相等，在加载/卸载段时间很短时，可以近似认为传感器在这一阶段蠕变为零，其输出变化量就是加在传感器上的载荷的变化量W0.设蠕变阶段载荷值和迅速卸载后零点值的差值为W1，基于上述蠕变和蠕变恢复是相等的假定，W1=W0.而电子天平称重值取载荷的差值W0，所以，判断出加载后蠕变点和蠕变恢复点就可以动态跟踪蠕变。具体算法如下：

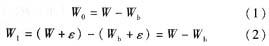
　　式中，W——天平加载后迅速达到S1点传感器输出值；W0——天平加载后迅速达到S1点天平称重值；Wb——天平空载或归零后零点值；W1——加载后蠕变和经蠕变修正后天平称重值；ε——蠕变动态值。

　　式（1）是加载到S1点天平的称重值；式（2）是加载稳定到S1点和进行蠕变补偿后天平的称重值，式中载荷蠕变和受加载影响天平零点蠕变值同是ε。？蠕变跟踪补偿的关键是判断和确定图1所示的S1点、蠕变量ε与时间的关系，然后根据这一关系进行蠕变补偿。补偿思路见图4.图4的前半段是确定S1点，后半段是蠕变跟踪处理。这里的关键问题是如何确定蠕变跟踪量和跟踪时间的关系。图1只定性地说明传感器的蠕变特性，但是，每个传感器都有定量的特性，也就是蠕变量ε与时间的关系。只有确定这一关系，才能确定蠕变跟踪时间和跟踪量（图4中的AD＿STA3）。解决的办法是在天平标定时一起确定蠕变曲线。具体做法是：加载砝码标定时按规程测试蠕变特性，单片机先记录下S1点，并记录每隔固定的时间段的当前A/D值与S1点的差值，这就是该段时间的蠕变值。用软件办法记录下这个传感器蠕变量与时间的关系，然后再根据这一关系确定跟踪量（AD＿STA-3）和跟踪时间。确定的原则是：固定的时间段蠕变量越大，跟踪量（AD＿STA-3）就越大和跟踪间隔时间就越小。反之，跟踪量（AD＿STA-3）就越小和跟踪间隔时间就越大。

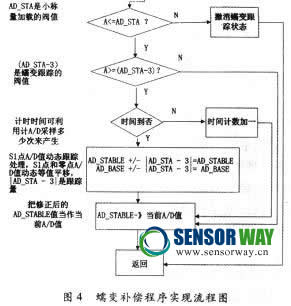
　　ING-TOP： 0px">通过对传感器工作状况和蠕变的分析，在测量过程中对蠕变误差进行实时跟踪，连续地对不同过程的蠕变量进行动态修正，因此，能实现高精度蠕变补偿。该方法只需在对天平标定时对传感器蠕变特性进行简易测试，补偿过程简单，无须人工干预，且补偿不受传感器载荷和温度影响。利用此方法设计的天平经多年批量投产证明，方法行之有效。

　　转载请注明来源：赛斯维传感器网（www.sensorway.cn）